Concord Carpenter

The 3-4-5 Method For Squaring Corners

By Robert Robillard on Home Repairs And Remodeling

Tweet

3-4-5 Triangle Method

Carpentry is not an exact science; it is a pragmatic approach to problem solving, building, and repairing. My experience has taught me that a few basic principles guide us on what will or will not work. Plumb, Level, and Square is some of those principles.

3-4-5 Rule To Ensure Square Layouts

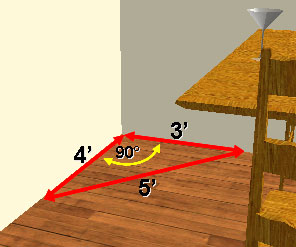
Carpenters and builders often use the 3-4-5 method for squaring corners and ensure that the projects they are building have a precise 90-degree angle.

In the residential and construction world carpenters often use speed squares and framing squares to check layouts.

When the layout is large these framing squares are simply too small to guarantee the accuracy needed. Large remodeling and construction projects such as laying out the foundation of a house or walls often employ a 3-4-5 triangle technique to ensure accurate 90-degree angles.

Avoid Compounding Errors

No matter what project you work on if your base or foundation is not level, plumb, and square the rest of your project will be off.   Errors at the base of a deck, house or porch will continue to grow and compound by the time you get to the finish trim, cabinets, or reach the roof framing.

3-4-5 Rule Layman’s Terms:

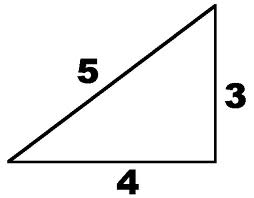
If the short side of the triangle is 3 feet, and the leg that extends from it 90 degrees is 4 feet, the hypotenuse, or longest leg, will be 5 feet.

This technique simply requires that the carpenter create a triangle in the corner of the lines that are to be square (90 degrees) to each other.

The 3-4-5 triangle must have

• One side ( triangle leg) that is 3 feet long
• A second side (triangle leg) that is 4 feet long
• A third side, connecting the two legs measuring 5 feet long

Any triangle with sides of 3, 4, and 5 feet will have a 90-degree angle opposite the 5-foot side.   The beauty and simplicity of this technique are if the carpenter or builder needs to increase accuracy on larger walls or structures, any multiple of the 3-4-5 rule can be deployed.

Examples of the 3-4-5 Rule

• 3-4-5
• 6-8-10
• 9-12-15
• 12- 16-20
• 15-20-25

Why Does This Work?

Mathematically why does the 3-4-5 method for squaring corners create a perfect right angle?

In Geometry, a well-known method of constructing the right angle is to employ the Pythagorean Theorem. The mathematician, Pythagoras, discovered a relationship between the sides of any right triangle that is now known as the Pythagorean Theorem. Pythagoras proved that the square of the longest side (the hypotenuse) is equal to the sum of the squares of the remaining two sides.

This is written as the following equation:

A and B are the two legs of the right triangle and C is the hypotenuse.  If we substitute the numbers from a 3-4-5 triangle into this formula, we then have 9″ + 16″ = 25″

Remembering the 3-4-5

Using triangle dimensions of 3, 4, and 5 is easy to remember and deploy. There are no difficult equations to remember and the 3-4-5 method will always produce a perfect right angle very time.